
Getting Started With Arduino
16th October 2020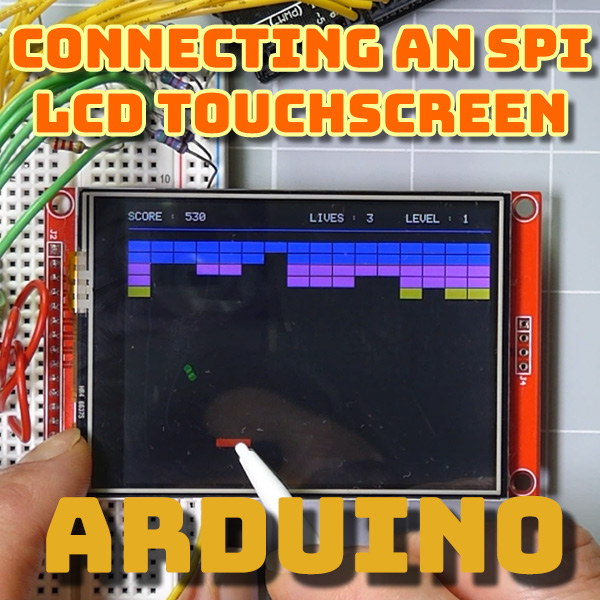
Connecting an SPI TFT Touchscreen to Your Arduino
23rd October 2020The 8 Queen (or N Queen) Problem in Computer Science
The 8 Queen Problem
This is one of the standard computer science problems that you’ll come across. It’s real aim is to test your algorithmic thinking and code optimisation skills.
The idea is that you have a chess board and eight queens. You have to place all eight queens onto the board so that no two queens are attacking each other.
If you’re not familiar with chess it’s a game played on an eight by eight grid of squares (the same as draughts or chequers!). A queen is one of the chess pieces that can move in straight lines; horizontally, vertically or diagonally. A queen is attacking any other square that she can move to, so no two queens can be horizontally, vertically or diagonally aligned.

So we have to design a computer program that will find all the possible solutions to the problem.
Using brute force and just trying out every possible combination of placing the queens on the board results in having to test 4,426,165,368 combinations. If we can process 50,000 combinations per second that’s going to take our computer over 24 hours to complete the task. We need a better solution!
We can start to work out ways of reducing this workload by examining the problem and optimising our algorithm.
One of the first things we can do is to notice that we can only place one queen on each row – as soon as we place a queen on a row, every other square in that row is under attack. So we now only have 8 * 8 * 8 * 8 * 8 * 8 * 8 * 8 combinations or 16,777,216.
If our algorithm works by placing a queen on the top row, then placing a queen on the second row, then on the third, we can eliminate blocks of combinations as soon as we find a combination of the first few rows that doesn’t work. For example placing a queen in the top right corner, followed by one directly beneath it doesn’t work. So all possible combinations that have queens in those two positions can be ignored. We then backtrack and place the second queen in the second square. Again this combination doesn’t work so we try the second queen in the third square. This time the queen is safe so we can progress to the third row and try the third queen in the first square, etc. This method of exploring all possible valid solutions by working along the solution until you get to an error and then stepping back to try an alternative solution is called a backtracking solution.
Coding the Solution
Once we’ve refined our algorithm we can code the 8 queen solution. In the video I use Python as the coding language.
Initially I talk you through a nested looping structure which solves the problem and finds the 92 solutions in under a second.
With that under your belt we then look at further refining the code to not only let us solve for 8 queens on an 8 x 8 board, but also for any number N queens on an N x N board. To do this we need to use a recursive algorithm.
A lot of people shy away from recursion as it can be tricky to get your head around how it works. But once you understand what’s needed recursion can become a very simple, elegant and efficient way of solving any nested structure problems. In the video you’ll see the whole problem shrink down to only about 30 lines of code using only a simple for / next loop.
Big O Complexity
For the looping solution we have a loop inside a loop inside a loop, etc. Each loop has complexity O(N) so the solution has complexity
T(N) = O(N) * O(N) * O(N) * O(N) * O(N) * O(N) * O(N) * O(N) = O(N^8)
For the recursive solution we have
T(N) = N * T(N-1) which simplifies down to O(N!)
Have fun!




