
Bounding Box Collision Detection (AABB) – Game Coding Tutorial
3rd January 2020
ZX Spectrum Jetpac – Retro Game Deconstruction
12th January 2020Bounding Ball Collision Detection – Game Coding Tutorial
In my previous tutorial we had a look at bounding box collision detection. We saw this was a great and fast way of getting fairly accurate collision detection providing that our objects more or less fitted into a rectangular area. But what of our objects aren’t rectangular or if they need to rotate. Quite often our bounding box solution ends up with either parts of the object sticking outside the box, or areas of our box which are empty, not containing an actual part of the object. In these situations we need a new solution.
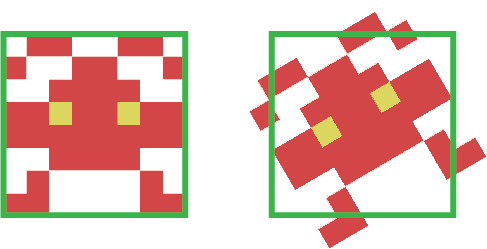
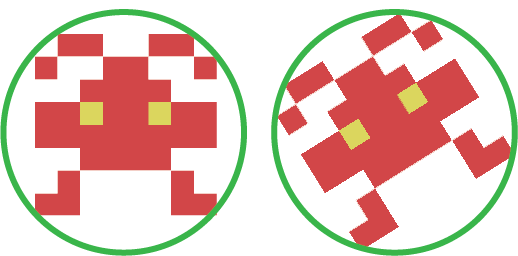
Bounding ball collision detection uses circles (balls) to surround our objects. Again we need to design our sprites and graphics so that they more or less fill their bounding ball. But once we’ve done this we are able to rotate them without parts coming outside our bounding lines.
To calculate if we have a collision we need to work out the distance between our objects. To do this we need to know the position of each object and the radius of its bounding ball.
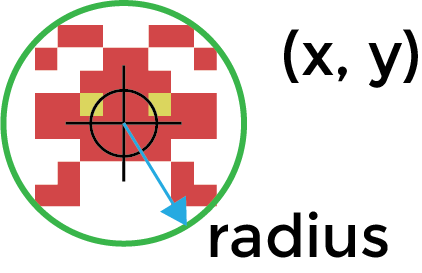
Usually the position of the object tells us the centre of the sprite or graphic. To calculate the distance between objects we simply need to apply Pythagoras theorem.
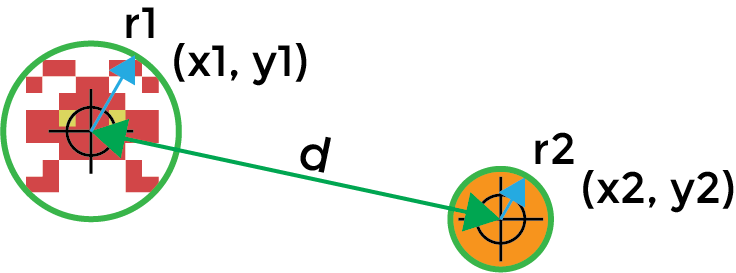
d = sqrt( (x2 – x1)2 + ( y2 – y1)2 )
Once we know the distance between objects we can compare this with the minimum distance between the two objects before they collide. This minimum distance is simply the sum of the two radii of the bounding balls.
r1 + r2
If the distance between the objects is less than or equal to this minimum distance then the objects have collided.
if (d <= (r1 + r2) )
// collision
As always we are trying to minimise the number of calculations needed to detect the collision. To get the actual distance between objects we need to use a square root function. This is quite costly in terms of processing power. We can get rid of this function by simply replacing it with a single multiplication. Instead of comparing the actual pixel distances, we can compare the squares of distances.
From Pythagoras we can quickly get the square of the distance between the objects by adding the squares of the X coordinate and Y coordinate separations. If we then square the minimum distance required between the objects we can compare this with the square of the separation to detect the collision. So our square root function gets replaced by multiplying the minimum distance by itself.
d2 = (x2 – x1)2 + ( y2 – y1)2
r2 = (r1 + r2) * (r1 + r2)
if ( d2 <= r2 )
// collision
With this optimisation our bounding ball collision detection only requires three multiplications, two additions and a comparison. It’s not quite as fast as the bounding box algorithm but it’s still very fast and therefore very suitable for course collision detection where we use a fast but slightly less accurate algorithm to work out which objects are close enough to collide before committing to one of our more accurate collision detection algorithms which requires much more processing power.
If you have a look at the demos below I’ve created a simple bounding ball collision detection example where you can move one of the circles and make it collide with the other circle.
The second demo is taken from the Asteroids programming course where we use the bounding ball algorithm to filter out asteroids which are too far away from any of the bullets before committing to the crossing number algorithm which accurately detects if a point has moved inside the polygon of the asteroid. I’ve slowed the demo down so you can see everything happening in real time. If you fire a bullet as an asteroid you’ll see the asteroid turn red once the bullet has entered the asteroids bounding ball. You should then see the bullet continue towards the asteroid until it actually crosses into the shape.
TIC80 Bounding Ball Collision Detection Demo
Click on the demo below and then use the cursor keys on your keyboard to move the blue circle.
Asteroids Using Ball Collision Detection for Course Detection Demo
Click on the demo below and then use the cursor keys on your keyboard to rotate and up to thrust. Z is the fire key.




